Conceitos sobre Estatística Aplicada à Testagem - Psicometria

A psicometria busca uma forma de mensurar fenômenos psicológicos para agregar maior valor para as ciências humana, no caso a psicologia. Com a objetividade das fórmulas aplicadas aos fenômenos humanos, busca-se uma melhor interpretação desses mesmos fenômenos através dos números, porém, somente o número, isolado, pouco nos representa; o número, ou o resultado do teste de um determinado fenômeno, deve estar acompanhado de um significado, sempre. Como disse, a psicometria é a área da psicologia que desenvolve técnicas de mensuração de fenômenos psicológicos, e, mensurar, é "medir algo atribuindo-lhe um significado". A vantagem da "medição" dentro da psicologia pode ser encarada como uma forma mais comunicável (dos resultados de pesquisas, difusão de conhecimento) e objetiva (dado mensurável significa que pode ser verificado por vários pesquisadores).

Mensurar: Medir, determinar uma medida, atribuir magnitude - Em nossa área atribuímos um significado para nosso resultado, mensuramos o fenômeno. Atribuímos magnitude a um objeto de acordo com certas regras, sistema numérico.

Teoria de Resposta ao Item (TRI):

 Podemos pensar que a TRI veio para derrubar a TCT (Teoria Clássica dos Testes), mas em análise críticas podemos ver que a TRI complementa a TCT.  Hoje, a Psicometria MODERNA resume-se à Teoria de Resposta ao Item e com isso quero dizer que, de forma geral, a TRI representa uma maior precisão na mensuração dos objetos qualificados e relevantes dessa área de estudo. Diferente da TCT, a TRI não se preocupa com o Escore Total de um determinado teste, ela busca especificamente por cada variável que determinaria esse Escore Total e quer saber qual é "a probabilidade e quais são os fatores que afetam esta probabilidade de cada item individualmente ser acertado ou errado (em testes de aptidão)" (Pasquali, 2009), ou de ser aceito ou rejeitado nos casos de testes de preferência (atitudes, personalidade, interesses). A TRI trabalha com traços latentes (características dos indivíduos que não podem ser medidas diretamente). Tal teoria analisa a probabilidade de um indivíduo acertar um item de acordo com sua proficiência ou traço latente.

Escore Total/Bruto: Soma das respostas certas, resultado obtido através dos testes (instrumentos de medida).

Por si só o Escore Total não nos representa muita coisa, Ex: Um escore alto poderá ser favorável num teste de habilidades, mas será desfavorável em testes que avaliam aspectos da personalidade da pessoa. É nesse contexto que a Teoria de Resposta ao Item fará sentido e mostrará porque se fez necessária a sua elaboração. A avaliação do Escore Total/Bruto está ligada a Teoria Clássica dos Teste que, como já explicamos, pouco mostra sobre determinados aspectos subjetivos.

 "Assim, a riqueza na avaliação psicológica ou educacional, dentro do enfoque da TRI, consiste em se conseguir construir armazéns de itens válidos para avaliar os traços latentes, armazéns estes chamados de bancos de itens para elaboração de um número sem fim de testes" (Pasquali, 2009).

Conceitos Básicos das Estatísticas na Psicometria:

Podemos ter "Estatística" como uma metodologia científica para a obtenção, organização e análise de dados. Nos é importante dois tipos de estatística:

Estatística Descritiva: Consiste numa metodologia que busca descrever, organizar e resumir os dados.

Estatística Inferencial: É o conjunto de métodos e técnicas estatísticas que procuram caracterizar ou INFERIR sobre uma população a partir de uma parte dela (amostra).

Exemplificando: temos uma determinada população e queremos INFERIR sobre ela, então coletaremos dados a partir de uma amostra, que constitui de parte dessa população. Agora, como sabemos que as pessoas da comunidade podem ser analisadas de diversos ângulos precisaremos determinar as variáveis, ex: Sexo, renda, habilidades, etc.

Estatística Descritiva: Por onde começo?

Antes de analisar os dados, nada melhor que organizá-los para facilitar nosso entendimento não é mesmo? Veja a imagem a seguir para que possamos dar continuidade: ela está organizada, na primeira linha temos a informação que temos dois números 11; ele apareceu duas vezes nos resultados.

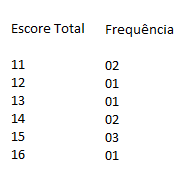
Note que temos os Escores Totais, que representam a quantidade de pontos acertados, e a Frequência ou a quantidade de pessoas que fizeram esses pontos (escore total). Agora precisamos saber onde a maior quantidade desses dados estão localizados e descobrir, também, seus valores centrais. Mas como? Basta aplicarmos uma medida de tendência central, que nada mais é que um valor central ou valor típico para uma distribuição de probabilidade. Chamamos essas medidas de Moda, Média e Mediana.

Medida de Tendência Central:

Moda: É o valor de ocorrência mais frequente em uma distribuição numérica, ou seja, é o valor que mais aparece em uma determinada "medida". Tome por exemplo essa sequência numérica: 1,1,2,3,3,3,6,7,7,8,8,8,8,9,9,9,10;

Qual é a moda dessa sequência? O número que mais aparece, certo?! Logo teremos o número 8 como a moda dessa sequência porque ele aparece 4x em relação aos outros. -> 1,1,2,3,3,3,6,7,7,8,8,8,8,9,9,9,10;

Nota: Só poderá haver uma moda ou, caso não houver variabilidade na distribuição. Caso houver dois números com valores de repetição igual (ex: 1,22,3,44) dizemos que a distribuição é bimodal ou multimodal.

Média: Talvez a mais fácil das Medidas de Tendência Central; A "Média" consiste em somar todos os valores de uma distribuição e dividir pelo total de valores somados. Veja na seguinte sequência: 1,2,3,6,7,8,9,10,13,14,16; Na prática ficará assim: 1+2+3+6+7+8+9+10+13+14+16 / 11, resultado 8.

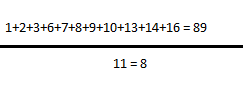
Veja que somamos todos os números apresentados e depois pegamos esse valor somado e dividimos pela quantidade desses números.

Mediana: Um pouco mais complicada que as duas últimas, porém, nada impossível de ser fazer. A mediana será o valor que divide em duas metades uma distribuição numérica, se contarmos a quantidade que aparecem em uma sequência e for ímpar, então o número que separa essa sequência será necessariamente o do meio. Caso essa sequência for par (total dos números, não confunda com a soma deles) então será os dois números do meio, que separam a sequência.

Exemplo: 2,3,5,6,8,10,12. Note que nessa sequência o 6 é o número que divide ela em dois, logo ele é a mediana dessa sequência; lembre-se que nesse caso a sequência é ímpar, porque tem 7 (nº ímpar) números. Vejamos com uma sequência par:

Exemplo: 20,23,25,26,27,30,31,40. Nessa sequência, que é par, a mediana será os dois números que dividem a sequência em dois, logo, a mediana será os números 26 e 27.

Exercício 01: Calcule a Moda, Média e Mediana da seguinte sequência: A) 2,5,2,3,6,7,3,2 - B) 1,3,2,1,6,3,8. (Veja a resposta no final do artigo)

Medida de Variabilidade:

Outro aspecto importante dentro do estudo descritivo de um conjunto de dados é o da determinação da variabilidade e/ou dispersão desses dados. Para determinar essa variabilidade e dispersão usamos dois termos: Variância e Desvio Padrão. Com esta estatística poderemos avaliar quanto de dispersão existe em m determinado conjunto (sequência, etc) de dados. A variabilidade é importante para destacar as diferenças individuais que são buscadas com os testes psicológicos. Com base nos resultados, então, poderemos tomar decisões em relação a uma determinada pessoa.

Variância: Será a média da soma dos quadrados de um determinado conjunto, Ex: 2,2; Logo 2² + 2² / 2 = 4. Note que elevamos cada número do conjunto ao quadrado 2 > 2² e depois somamos esses resultados e dividimos pela quantidade de números somados.

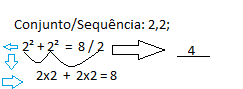
Desvio Padrão: O desvio padrão é a raiz quadrada da variância.

Resposta: A) Moda, 2; Mediana, 3 e 6; Média, 3. - B) Moda, 1 e 2 Bimodal ou Multimodal; Mediana, 1; Média, 3.

Referências:

Paquali, Luiz. Psychometrics. Scielo: São Paulo, 2009.